Градієнтне зафарбовування
Лінійне і радіальне зафарбовування представлено у jsFiddle.
Градієнти вказуються в окремому тезі - <defs>
Кожен градієнт містить стоп-точки, між якими колір плавно переходить з одного в інший.
<linearGradient>
<radialGradient>
id - ідентифікатор градієнта, до якого звертаються примітиви, щоб отримати зафарбовування.
<stop> - стоп-точка кольору.
offset="0%" - положення стоп-точки; повинно бути щонайменше 2 точки з положеннями 0% і 100%.
stop-color="red" - колір стоп-точки.
stop-opacity="1" - прозорість стоп-точки.
Градієнти ще мають декілька налаштувань, типу фокальної точки, повторення і т.п.
Завдання
- Сервер видає дані про популярність поросят в інтернеті у вигляді JSON-файла.
Побудуйте графік популярності поросят за тиждень. - Побудуйте кругову діаграму сумарної популярності поросят у процентах.
Задача про прямокутний трикутник
У завданні про кругову діаграму щоб використовувати дуги потрібно знати кінцеву точку дуги.
Ще один ньюанс - на полотні відлік градусів починається від осі X (третя година по годиннику), а в кругових діаграмах - від вертикалі (дванадцята година по годиннику). Не забудьте згодом закласти цю поправку у -90 градусів.
Отже, нам потрібно створити path з лінії від центру кола до його окружності, провести по окружності дугу на певний градус (але нам потрібні координати кінцевої точки) і намалювати лінію до центру кола.
Отримуємо класичну задачу на трикутники:
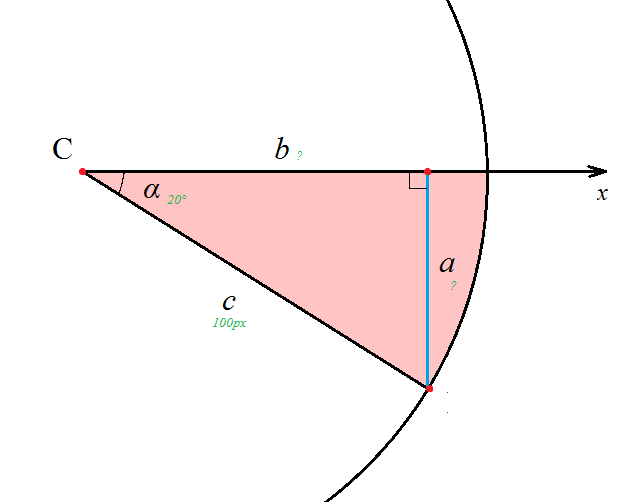
Маємо прямокутний трикутник з вершиною C в центрі кола, гіпотенузою c, двома катетами a та b і кутом α проти катета a.
З цього набору даних нам відомі координати точки C, довжина гіпотенузи (радіус нашої діаграми) та кут α, який ми вирахували через пропорційне співвідношення популярності кожного поросяти до суми їх популярностей.
Нам потрібно вирахувати довжину катетів a та b - це буде зсув координати кінця дуги по осям y та x відносно точки C.
Згадаємо чи загуглимо задачі про трикутники. Нам допоможуть sin та cos:
Синус кута - відношеня протилеглого катета до гіпотинузи.
sin(α) = a / c
Косинус кута - відношення прилеглого катета до гіпотинузи.
cos(α) = b / c
Ну і далі - все просто, виводимо формули для знаходження a та b, підставляємо у формули радіус та потрібний кут і результати використовуємо у path.